`pygad` Module¶

This section of the PyGAD’s library documentation discusses the pygad module.

Using the pygad module, instances of the genetic algorithm can be created, run, saved, and loaded. Single-objective and multi-objective optimization problems can be solved.

`pygad.GA` Class¶

The first module available in PyGAD is named pygad and contains a class named GA for building the genetic algorithm. The constructor, methods, function, and attributes within the class are discussed in this section.

`init()`¶

For creating an instance of the pygad.GA class, the constructor accepts several parameters that allow the user to customize the genetic algorithm to different types of applications.

The pygad.GA class constructor supports the following parameters:

num_generations: Number of generations.
num_parents_mating: Number of solutions to be selected as parents.
fitness_func: Accepts a function/method and returns the fitness value(s) of the solution. If a function is passed, then it must accept 3 parameters (1. the instance of the pygad.GA class, 2. a single solution, and 3. its index in the population). If method, then it accepts a fourth parameter representing the method’s class instance. Check the Preparing the fitness_func Parameter section for information about creating such a function. In PyGAD 3.2.0, multi-objective optimization is supported. To consider the problem as multi-objective, just return a list, tuple, or numpy.ndarray from the fitness function.
fitness_batch_size=None: A new optional parameter called fitness_batch_size is supported to calculate the fitness function in batches. If it is assigned the value 1 or None (default), then the normal flow is used where the fitness function is called for each individual solution. If the fitness_batch_size parameter is assigned a value satisfying this condition 1 < fitness_batch_size <= sol_per_pop, then the solutions are grouped into batches of size fitness_batch_size and the fitness function is called once for each batch. Check the Batch Fitness Calculation section for more details and examples. Added in from PyGAD 2.19.0.
initial_population: A user-defined initial population. It is useful when the user wants to start the generations with a custom initial population. It defaults to None which means no initial population is specified by the user. In this case, PyGAD creates an initial population using the sol_per_pop and num_genes parameters. An exception is raised if the initial_population is None while any of the 2 parameters (sol_per_pop or num_genes) is also None. Introduced in PyGAD 2.0.0 and higher.
sol_per_pop: Number of solutions (i.e. chromosomes) within the population. This parameter has no action if initial_population parameter exists.
num_genes: Number of genes in the solution/chromosome. This parameter is not needed if the user feeds the initial population to the initial_population parameter.
gene_type=float: Controls the gene type. It can be assigned to a single data type that is applied to all genes or can specify the data type of each individual gene. It defaults to float which means all genes are of float data type. Starting from PyGAD 2.9.0, the gene_type parameter can be assigned to a numeric value of any of these types: int, float, and numpy.int/uint/float(8-64). Starting from PyGAD 2.14.0, it can be assigned to a list, tuple, or a numpy.ndarray which hold a data type for each gene (e.g. gene_type=[int, float, numpy.int8]). This helps to control the data type of each individual gene. In PyGAD 2.15.0, a precision for the float data types can be specified (e.g. gene_type=[float, 2].
init_range_low=-4: The lower value of the random range from which the gene values in the initial population are selected. init_range_low defaults to -4. Available in PyGAD 1.0.20 and higher. This parameter has no action if the initial_population parameter exists.
init_range_high=4: The upper value of the random range from which the gene values in the initial population are selected. init_range_high defaults to +4. Available in PyGAD 1.0.20 and higher. This parameter has no action if the initial_population parameter exists.
parent_selection_type="sss": The parent selection type. Supported types are sss (for steady-state selection), rws (for roulette wheel selection), sus (for stochastic universal selection), rank (for rank selection), random (for random selection), and tournament (for tournament selection). A custom parent selection function can be passed starting from PyGAD 2.16.0. Check the User-Defined Crossover, Mutation, and Parent Selection Operators section for more details about building a user-defined parent selection function.
keep_parents=-1: Number of parents to keep in the current population. -1 (default) means to keep all parents in the next population. 0 means keep no parents in the next population. A value greater than 0 means keeps the specified number of parents in the next population. Note that the value assigned to keep_parents cannot be < - 1 or greater than the number of solutions within the population sol_per_pop. Starting from PyGAD 2.18.0, this parameter have an effect only when the keep_elitism parameter is 0. Starting from PyGAD 2.20.0, the parents’ fitness from the last generation will not be re-used if keep_parents=0.
keep_elitism=1: Added in PyGAD 2.18.0. It can take the value 0 or a positive integer that satisfies (0 <= keep_elitism <= sol_per_pop). It defaults to 1 which means only the best solution in the current generation is kept in the next generation. If assigned 0, this means it has no effect. If assigned a positive integer K, then the best K solutions are kept in the next generation. It cannot be assigned a value greater than the value assigned to the sol_per_pop parameter. If this parameter has a value different than 0, then the keep_parents parameter will have no effect.
K_tournament=3: In case that the parent selection type is tournament, the K_tournament specifies the number of parents participating in the tournament selection. It defaults to 3.
crossover_type="single_point": Type of the crossover operation. Supported types are single_point (for single-point crossover), two_points (for two points crossover), uniform (for uniform crossover), and scattered (for scattered crossover). Scattered crossover is supported from PyGAD 2.9.0 and higher. It defaults to single_point. A custom crossover function can be passed starting from PyGAD 2.16.0. Check the User-Defined Crossover, Mutation, and Parent Selection Operators section for more details about creating a user-defined crossover function. Starting from PyGAD 2.2.2 and higher, if crossover_type=None, then the crossover step is bypassed which means no crossover is applied and thus no offspring will be created in the next generations. The next generation will use the solutions in the current population.
crossover_probability=None: The probability of selecting a parent for applying the crossover operation. Its value must be between 0.0 and 1.0 inclusive. For each parent, a random value between 0.0 and 1.0 is generated. If this random value is less than or equal to the value assigned to the crossover_probability parameter, then the parent is selected. Added in PyGAD 2.5.0 and higher.
mutation_type="random": Type of the mutation operation. Supported types are random (for random mutation), swap (for swap mutation), inversion (for inversion mutation), scramble (for scramble mutation), and adaptive (for adaptive mutation). It defaults to random. A custom mutation function can be passed starting from PyGAD 2.16.0. Check the User-Defined Crossover, Mutation, and Parent Selection Operators section for more details about creating a user-defined mutation function. Starting from PyGAD 2.2.2 and higher, if mutation_type=None, then the mutation step is bypassed which means no mutation is applied and thus no changes are applied to the offspring created using the crossover operation. The offspring will be used unchanged in the next generation. Adaptive mutation is supported starting from PyGAD 2.10.0. For more information about adaptive mutation, go the the Adaptive Mutation section. For example about using adaptive mutation, check the Use Adaptive Mutation in PyGAD section.
mutation_probability=None: The probability of selecting a gene for applying the mutation operation. Its value must be between 0.0 and 1.0 inclusive. For each gene in a solution, a random value between 0.0 and 1.0 is generated. If this random value is less than or equal to the value assigned to the mutation_probability parameter, then the gene is selected. If this parameter exists, then there is no need for the 2 parameters mutation_percent_genes and mutation_num_genes. Added in PyGAD 2.5.0 and higher.
mutation_by_replacement=False: An optional bool parameter. It works only when the selected type of mutation is random (mutation_type="random"). In this case, mutation_by_replacement=True means replace the gene by the randomly generated value. If False, then it has no effect and random mutation works by adding the random value to the gene. Supported in PyGAD 2.2.2 and higher. Check the changes in PyGAD 2.2.2 under the Release History section for an example.
mutation_percent_genes="default": Percentage of genes to mutate. It defaults to the string "default" which is later translated into the integer 10 which means 10% of the genes will be mutated. It must be >0 and <=100. Out of this percentage, the number of genes to mutate is deduced which is assigned to the mutation_num_genes parameter. The mutation_percent_genes parameter has no action if mutation_probability or mutation_num_genes exist. Starting from PyGAD 2.2.2 and higher, this parameter has no action if mutation_type is None.
mutation_num_genes=None: Number of genes to mutate which defaults to None meaning that no number is specified. The mutation_num_genes parameter has no action if the parameter mutation_probability exists. Starting from PyGAD 2.2.2 and higher, this parameter has no action if mutation_type is None.
random_mutation_min_val=-1.0: For random mutation, the random_mutation_min_val parameter specifies the start value of the range from which a random value is selected to be added to the gene. It defaults to -1. Starting from PyGAD 2.2.2 and higher, this parameter has no action if mutation_type is None.
random_mutation_max_val=1.0: For random mutation, the random_mutation_max_val parameter specifies the end value of the range from which a random value is selected to be added to the gene. It defaults to +1. Starting from PyGAD 2.2.2 and higher, this parameter has no action if mutation_type is None.
gene_space=None: It is used to specify the possible values for each gene in case the user wants to restrict the gene values. It is useful if the gene space is restricted to a certain range or to discrete values. It accepts a list, range, or numpy.ndarray. When all genes have the same global space, specify their values as a list/tuple/range/numpy.ndarray. For example, gene_space = [0.3, 5.2, -4, 8] restricts the gene values to the 4 specified values. If each gene has its own space, then the gene_space parameter can be nested like [[0.4, -5], [0.5, -3.2, 8.2, -9], ...] where the first sublist determines the values for the first gene, the second sublist for the second gene, and so on. If the nested list/tuple has a None value, then the gene’s initial value is selected randomly from the range specified by the 2 parameters init_range_low and init_range_high and its mutation value is selected randomly from the range specified by the 2 parameters random_mutation_min_val and random_mutation_max_val. gene_space is added in PyGAD 2.5.0. Check the Release History of PyGAD 2.5.0 section of the documentation for more details. In PyGAD 2.9.0, NumPy arrays can be assigned to the gene_space parameter. In PyGAD 2.11.0, the gene_space parameter itself or any of its elements can be assigned to a dictionary to specify the lower and upper limits of the genes. For example, {'low': 2, 'high': 4} means the minimum and maximum values are 2 and 4, respectively. In PyGAD 2.15.0, a new key called "step" is supported to specify the step of moving from the start to the end of the range specified by the 2 existing keys "low" and "high".
on_start=None: Accepts a function/method to be called only once before the genetic algorithm starts its evolution. If function, then it must accept a single parameter representing the instance of the genetic algorithm. If method, then it must accept 2 parameters where the second one refers to the method’s object. Added in PyGAD 2.6.0.
on_fitness=None: Accepts a function/method to be called after calculating the fitness values of all solutions in the population. If function, then it must accept 2 parameters: 1) a list of all solutions’ fitness values 2) the instance of the genetic algorithm. If method, then it must accept 3 parameters where the third one refers to the method’s object. Added in PyGAD 2.6.0.
on_parents=None: Accepts a function/method to be called after selecting the parents that mates. If function, then it must accept 2 parameters: 1) the selected parents 2) the instance of the genetic algorithm If method, then it must accept 3 parameters where the third one refers to the method’s object. Added in PyGAD 2.6.0.
on_crossover=None: Accepts a function to be called each time the crossover operation is applied. This function must accept 2 parameters: the first one represents the instance of the genetic algorithm and the second one represents the offspring generated using crossover. Added in PyGAD 2.6.0.
on_mutation=None: Accepts a function to be called each time the mutation operation is applied. This function must accept 2 parameters: the first one represents the instance of the genetic algorithm and the second one represents the offspring after applying the mutation. Added in PyGAD 2.6.0.
on_generation=None: Accepts a function to be called after each generation. This function must accept a single parameter representing the instance of the genetic algorithm. If the function returned the string stop, then the run() method stops without completing the other generations. Added in PyGAD 2.6.0.
on_stop=None: Accepts a function to be called only once exactly before the genetic algorithm stops or when it completes all the generations. This function must accept 2 parameters: the first one represents the instance of the genetic algorithm and the second one is a list of fitness values of the last population’s solutions. Added in PyGAD 2.6.0.
delay_after_gen=0.0: It accepts a non-negative number specifying the time in seconds to wait after a generation completes and before going to the next generation. It defaults to 0.0 which means no delay after the generation. Available in PyGAD 2.4.0 and higher.
save_best_solutions=False: When True, then the best solution after each generation is saved into an attribute named best_solutions. If False (default), then no solutions are saved and the best_solutions attribute will be empty. Supported in PyGAD 2.9.0.
save_solutions=False: If True, then all solutions in each generation are appended into an attribute called solutions which is NumPy array. Supported in PyGAD 2.15.0.
suppress_warnings=False: A bool parameter to control whether the warning messages are printed or not. It defaults to False.
allow_duplicate_genes=True: Added in PyGAD 2.13.0. If True, then a solution/chromosome may have duplicate gene values. If False, then each gene will have a unique value in its solution.
stop_criteria=None: Some criteria to stop the evolution. Added in PyGAD 2.15.0. Each criterion is passed as str which has a stop word. The current 2 supported words are reach and saturate. reach stops the run() method if the fitness value is equal to or greater than a given fitness value. An example for reach is "reach_40" which stops the evolution if the fitness is >= 40. saturate means stop the evolution if the fitness saturates for a given number of consecutive generations. An example for saturate is "saturate_7" which means stop the run() method if the fitness does not change for 7 consecutive generations.
parallel_processing=None: Added in PyGAD 2.17.0. If None (Default), this means no parallel processing is applied. It can accept a list/tuple of 2 elements [1) Can be either 'process' or 'thread' to indicate whether processes or threads are used, respectively., 2) The number of processes or threads to use.]. For example, parallel_processing=['process', 10] applies parallel processing with 10 processes. If a positive integer is assigned, then it is used as the number of threads. For example, parallel_processing=5 uses 5 threads which is equivalent to parallel_processing=["thread", 5]. For more information, check the Parallel Processing in PyGAD section.
random_seed=None: Added in PyGAD 2.18.0. It defines the random seed to be used by the random function generators (we use random functions in the NumPy and random modules). This helps to reproduce the same results by setting the same random seed (e.g. random_seed=2). If given the value None, then it has no effect.
logger=None: Accepts an instance of the logging.Logger class to log the outputs. Any message is no longer printed using print() but logged. If logger=None, then a logger is created that uses StreamHandler to logs the messages to the console. Added in PyGAD 3.0.0. Check the Logging Outputs for more information.

The user doesn’t have to specify all of such parameters while creating an instance of the GA class. A very important parameter you must care about is fitness_func which defines the fitness function.

It is OK to set the value of any of the 2 parameters init_range_low and init_range_high to be equal, higher, or lower than the other parameter (i.e. init_range_low is not needed to be lower than init_range_high). The same holds for the random_mutation_min_val and random_mutation_max_val parameters.

If the 2 parameters mutation_type and crossover_type are None, this disables any type of evolution the genetic algorithm can make. As a result, the genetic algorithm cannot find a better solution that the best solution in the initial population.

The parameters are validated within the constructor. If at least a parameter is not correct, an exception is thrown.

Plotting Methods in `pygad.GA` Class¶

plot_fitness(): Shows how the fitness evolves by generation.
plot_genes(): Shows how the gene value changes for each generation.
plot_new_solution_rate(): Shows the number of new solutions explored in each solution.

Class Attributes¶

supported_int_types: A list of the supported types for the integer numbers.
supported_float_types: A list of the supported types for the floating-point numbers.
supported_int_float_types: A list of the supported types for all numbers. It just concatenates the previous 2 lists.

Other Instance Attributes & Methods¶

All the parameters and functions passed to the pygad.GA class constructor are used as class attributes and methods in the instances of the pygad.GA class. In addition to such attributes, there are other attributes and methods added to the instances of the pygad.GA class:

The next 2 subsections list such attributes and methods.

Other Attributes¶

generations_completed: Holds the number of the last completed generation.
population: A NumPy array holding the initial population.
valid_parameters: Set to True when all the parameters passed in the GA class constructor are valid.
run_completed: Set to True only after the run() method completes gracefully.
pop_size: The population size.
best_solutions_fitness: A list holding the fitness values of the best solutions for all generations.
best_solution_generation: The generation number at which the best fitness value is reached. It is only assigned the generation number after the run() method completes. Otherwise, its value is -1.
best_solutions: A NumPy array holding the best solution per each generation. It only exists when the save_best_solutions parameter in the pygad.GA class constructor is set to True.
last_generation_fitness: The fitness values of the solutions in the last generation. Added in PyGAD 2.12.0.
previous_generation_fitness: At the end of each generation, the fitness of the most recent population is saved in the last_generation_fitness attribute. The fitness of the population exactly preceding this most recent population is saved in the last_generation_fitness attribute. This previous_generation_fitness attribute is used to fetch the pre-calculated fitness instead of calling the fitness function for already explored solutions. Added in PyGAD 2.16.2.
last_generation_parents: The parents selected from the last generation. Added in PyGAD 2.12.0.
last_generation_offspring_crossover: The offspring generated after applying the crossover in the last generation. Added in PyGAD 2.12.0.
last_generation_offspring_mutation: The offspring generated after applying the mutation in the last generation. Added in PyGAD 2.12.0.
gene_type_single: A flag that is set to True if the gene_type parameter is assigned to a single data type that is applied to all genes. If gene_type is assigned a list, tuple, or numpy.ndarray, then the value of gene_type_single will be False. Added in PyGAD 2.14.0.
last_generation_parents_indices: This attribute holds the indices of the selected parents in the last generation. Supported in PyGAD 2.15.0.
last_generation_elitism: This attribute holds the elitism of the last generation. It is effective only if the keep_elitism parameter has a non-zero value. Supported in PyGAD 2.18.0.
last_generation_elitism_indices: This attribute holds the indices of the elitism of the last generation. It is effective only if the keep_elitism parameter has a non-zero value. Supported in PyGAD 2.19.0.
logger: This attribute holds the logger from the logging module. Supported in PyGAD 3.0.0.
gene_space_unpacked: This is the unpacked version of the gene_space parameter. For example, range(1, 5) is unpacked to [1, 2, 3, 4]. For an infinite range like {'low': 2, 'high': 4}, then it is unpacked to a limited number of values (e.g. 100). Supported in PyGAD 3.1.0.
pareto_fronts: A new instance attribute named pareto_fronts added to the pygad.GA instances that holds the pareto fronts when solving a multi-objective problem. Supported in PyGAD 3.2.0.

Note that the attributes with names starting with last_generation_ are updated after each generation.

Other Methods¶

cal_pop_fitness(): A method that calculates the fitness values for all solutions within the population by calling the function passed to the fitness_func parameter for each solution.
crossover(): Refers to the method that applies the crossover operator based on the selected type of crossover in the crossover_type property.
mutation(): Refers to the method that applies the mutation operator based on the selected type of mutation in the mutation_type property.
select_parents(): Refers to a method that selects the parents based on the parent selection type specified in the parent_selection_type attribute.
adaptive_mutation_population_fitness(): Returns the average fitness value used in the adaptive mutation to filter the solutions.
summary(): Prints a Keras-like summary of the PyGAD lifecycle. This helps to have an overview of the architecture. Supported in PyGAD 2.19.0. Check the Print Lifecycle Summary section for more details and examples.
4 methods with names starting with run_. Their purpose is to keep the main loop inside the run() method clean. The details inside the loop are moved to 4 individual methods. Generally, any method with a name starting with run_ is meant to be called by PyGAD from inside the run() method. Supported in PyGAD 3.3.1.
1. run_select_parents(call_on_parents=True): Select the parents and call the callable on_parents() if defined. If call_on_parents is True, then the callable on_parents() is called. It must be False when the run_select_parents() method is called to update the parents at the end of the run() method.
2. run_crossover(): Apply crossover and call the callable on_crossover() if defined.
3. run_mutation(): Apply mutation and call the callable on_mutation() if defined.
4. run_update_population(): Update the population attribute after completing the processes of crossover and mutation.

The next sections discuss the methods available in the pygad.GA class.

`initialize_population()`¶

It creates an initial population randomly as a NumPy array. The array is saved in the instance attribute named population.

Accepts the following parameters:

low: The lower value of the random range from which the gene values in the initial population are selected. It defaults to -4. Available in PyGAD 1.0.20 and higher.
high: The upper value of the random range from which the gene values in the initial population are selected. It defaults to -4. Available in PyGAD 1.0.20.

This method assigns the values of the following 3 instance attributes:

pop_size: Size of the population.
population: Initially, it holds the initial population and later updated after each generation.
initial_population: Keeping the initial population.

`cal_pop_fitness()`¶

The cal_pop_fitness() method calculates and returns the fitness values of the solutions in the current population.

This function is optimized to save time by making fewer calls the fitness function. It follows this process:

If the save_solutions parameter is set to True, then it checks if the solution is already explored and saved in the solutions instance attribute. If so, then it just retrieves its fitness from the solutions_fitness instance attribute without calling the fitness function.
If save_solutions is set to False or if it is True but the solution was not explored yet, then the cal_pop_fitness() method checks if the keep_elitism parameter is set to a positive integer. If so, then it checks if the solution is saved into the last_generation_elitism instance attribute. If so, then it retrieves its fitness from the previous_generation_fitness instance attribute.
If neither of the above 3 conditions apply (1. save_solutions is set to False or 2. if it is True but the solution was not explored yet or 3. keep_elitism is set to zero), then the cal_pop_fitness() method checks if the keep_parents parameter is set to -1 or a positive integer. If so, then it checks if the solution is saved into the last_generation_parents instance attribute. If so, then it retrieves its fitness from the previous_generation_fitness instance attribute.
If neither of the above 4 conditions apply, then we have to call the fitness function to calculate the fitness for the solution. This is by calling the function assigned to the fitness_func parameter.

This function takes into consideration:

The parallel_processing parameter to check whether parallel processing is in effect.
The fitness_batch_size parameter to check if the fitness should be calculated in batches of solutions.

It returns a vector of the solutions’ fitness values.

`run()`¶

Runs the genetic algorithm. This is the main method in which the genetic algorithm is evolved through some generations. It accepts no parameters as it uses the instance to access all of its requirements.

For each generation, the fitness values of all solutions within the population are calculated according to the cal_pop_fitness() method which internally just calls the function assigned to the fitness_func parameter in the pygad.GA class constructor for each solution.

According to the fitness values of all solutions, the parents are selected using the select_parents() method. This method behaviour is determined according to the parent selection type in the parent_selection_type parameter in the pygad.GA class constructor

Based on the selected parents, offspring are generated by applying the crossover and mutation operations using the crossover() and mutation() methods. The behaviour of such 2 methods is defined according to the crossover_type and mutation_type parameters in the pygad.GA class constructor.

After the generation completes, the following takes place:

The population attribute is updated by the new population.
The generations_completed attribute is assigned by the number of the last completed generation.
If there is a callback function assigned to the on_generation attribute, then it will be called.

After the run() method completes, the following takes place:

The best_solution_generation is assigned the generation number at which the best fitness value is reached.
The run_completed attribute is set to True.

Parent Selection Methods¶

The ParentSelection class in the pygad.utils.parent_selection module has several methods for selecting the parents that will mate to produce the offspring. All of such methods accept the same parameters which are:

fitness: The fitness values of the solutions in the current population.
num_parents: The number of parents to be selected.

All of such methods return an array of the selected parents.

The next subsections list the supported methods for parent selection.

`steady_state_selection()`¶

Selects the parents using the steady-state selection technique.

`rank_selection()`¶

Selects the parents using the rank selection technique.

`random_selection()`¶

Selects the parents randomly.

`tournament_selection()`¶

Selects the parents using the tournament selection technique.

`roulette_wheel_selection()`¶

Selects the parents using the roulette wheel selection technique.

`stochastic_universal_selection()`¶

Selects the parents using the stochastic universal selection technique.

`nsga2_selection()`¶

Selects the parents for the NSGA-II algorithm to solve multi-objective optimization problems. It selects the parents by ranking them based on non-dominated sorting and crowding distance.

`tournament_selection_nsga2()`¶

Selects the parents for the NSGA-II algorithm to solve multi-objective optimization problems. It selects the parents using the tournament selection technique applied based on non-dominated sorting and crowding distance.

Crossover Methods¶

The Crossover class in the pygad.utils.crossover module supports several methods for applying crossover between the selected parents. All of these methods accept the same parameters which are:

parents: The parents to mate for producing the offspring.
offspring_size: The size of the offspring to produce.

All of such methods return an array of the produced offspring.

The next subsections list the supported methods for crossover.

`single_point_crossover()`¶

Applies the single-point crossover. It selects a point randomly at which crossover takes place between the pairs of parents.

`two_points_crossover()`¶

Applies the 2 points crossover. It selects the 2 points randomly at which crossover takes place between the pairs of parents.

`uniform_crossover()`¶

Applies the uniform crossover. For each gene, a parent out of the 2 mating parents is selected randomly and the gene is copied from it.

`scattered_crossover()`¶

Applies the scattered crossover. It randomly selects the gene from one of the 2 parents.

Mutation Methods¶

The Mutation class in the pygad.utils.mutation module supports several methods for applying mutation. All of these methods accept the same parameter which is:

offspring: The offspring to mutate.

All of such methods return an array of the mutated offspring.

The next subsections list the supported methods for mutation.

`random_mutation()`¶

Applies the random mutation which changes the values of some genes randomly. The number of genes is specified according to either the mutation_num_genes or the mutation_percent_genes attributes.

For each gene, a random value is selected according to the range specified by the 2 attributes random_mutation_min_val and random_mutation_max_val. The random value is added to the selected gene.

`swap_mutation()`¶

Applies the swap mutation which interchanges the values of 2 randomly selected genes.

`inversion_mutation()`¶

Applies the inversion mutation which selects a subset of genes and inverts them.

`scramble_mutation()`¶

Applies the scramble mutation which selects a subset of genes and shuffles their order randomly.

`adaptive_mutation()`¶

Applies the adaptive mutation which selects the number/percentage of genes to mutate based on the solution’s fitness. If the fitness is high (i.e. solution quality is high), then small number/percentage of genes is mutated compared to a solution with a low fitness.

`best_solution()`¶

Returns information about the best solution found by the genetic algorithm.

It accepts the following parameters:

pop_fitness=None: An optional parameter that accepts a list of the fitness values of the solutions in the population. If None, then the cal_pop_fitness() method is called to calculate the fitness values of the population.

It returns the following:

best_solution: Best solution in the current population.
best_solution_fitness: Fitness value of the best solution.
best_match_idx: Index of the best solution in the current population.

`plot_fitness()`¶

Previously named plot_result(), this method creates, shows, and returns a figure that summarizes how the fitness value evolves by generation.

It works only after completing at least 1 generation. If no generation is completed (at least 1), an exception is raised.

`plot_new_solution_rate()`¶

The plot_new_solution_rate() method creates, shows, and returns a figure that shows the number of new solutions explored in each generation. This method works only when save_solutions=True in the constructor of the pygad.GA class.

It works only after completing at least 1 generation. If no generation is completed (at least 1), an exception is raised.

`plot_genes()`¶

The plot_genes() method creates, shows, and returns a figure that describes each gene. It has different options to create the figures which helps to:

Explore the gene value for each generation by creating a normal plot.
Create a histogram for each gene.
Create a boxplot.

This is controlled by the graph_type parameter.

It works only after completing at least 1 generation. If no generation is completed (at least 1), an exception is raised.

`save()`¶

Saves the genetic algorithm instance

Accepts the following parameter:

filename: Name of the file to save the instance. No extension is needed.

Functions in `pygad`¶

Besides the methods available in the pygad.GA class, this section discusses the functions available in pygad. Up to this time, there is only a single function named load().

`pygad.load()`¶

Reads a saved instance of the genetic algorithm. This is not a method but a function that is indented under the pygad module. So, it could be called by the pygad module as follows: pygad.load(filename).

Accepts the following parameter:

filename: Name of the file holding the saved instance of the genetic algorithm. No extension is needed.

Returns the genetic algorithm instance.

Steps to Use `pygad`¶

To use the pygad module, here is a summary of the required steps:

Preparing the fitness_func parameter.
Preparing Other Parameters.
Import pygad.
Create an Instance of the pygad.GA Class.
Run the Genetic Algorithm.
Plotting Results.
Information about the Best Solution.
Saving & Loading the Results.

Let’s discuss how to do each of these steps.

Preparing the `fitness_func` Parameter¶

Even though some steps in the genetic algorithm pipeline can work the same regardless of the problem being solved, one critical step is the calculation of the fitness value. There is no unique way of calculating the fitness value and it changes from one problem to another.

PyGAD has a parameter called fitness_func that allows the user to specify a custom function/method to use when calculating the fitness. This function/method must be a maximization function/method so that a solution with a high fitness value returned is selected compared to a solution with a low value.

The fitness function is where the user can decide whether the optimization problem is single-objective or multi-objective.

If the fitness function returns a numeric value, then the problem is single-objective. The numeric data types supported by PyGAD are listed in the supported_int_float_types variable of the pygad.GA class.
If the fitness function returns a list, tuple, or numpy.ndarray, then the problem is multi-objective. Even if there is only one element, the problem is still considered multi-objective. Each element represents the fitness value of its corresponding objective.

Using a user-defined fitness function allows the user to freely use PyGAD to solve any problem by passing the appropriate fitness function/method. It is very important to understand the problem well before creating it.

Let’s discuss an example:

Given the following function:

y = f(w1:w6) = w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + 6wx6

where (x1,x2,x3,x4,x5,x6)=(4, -2, 3.5, 5, -11, -4.7) and y=44

What are the best values for the 6 weights (w1 to w6)? We are going to use the genetic algorithm to optimize this function.

So, the task is about using the genetic algorithm to find the best values for the 6 weight W1 to W6. Thinking of the problem, it is clear that the best solution is that returning an output that is close to the desired output y=44. So, the fitness function/method should return a value that gets higher when the solution’s output is closer to y=44. Here is a function that does that:

function_inputs = [4, -2, 3.5, 5, -11, -4.7] # Function inputs.
desired_output = 44 # Function output.

def fitness_func(ga_instance, solution, solution_idx):
    output = numpy.sum(solution*function_inputs)
    fitness = 1.0 / numpy.abs(output - desired_output)
    return fitness

Because the fitness function returns a numeric value, then the problem is single-objective.

Such a user-defined function must accept 3 parameters:

The instance of the pygad.GA class. This helps the user to fetch any property that helps when calculating the fitness.
The solution(s) to calculate the fitness value(s). Note that the fitness function can accept multiple solutions only if the fitness_batch_size is given a value greater than 1.
The indices of the solutions in the population. The number of indices also depends on the fitness_batch_size parameter.

If a method is passed to the fitness_func parameter, then it accepts a fourth parameter representing the method’s instance.

The __code__ object is used to check if this function accepts the required number of parameters. If more or fewer parameters are passed, an exception is thrown.

By creating this function, you did a very important step towards using PyGAD.

Preparing Other Parameters¶

Here is an example for preparing the other parameters:

num_generations = 50
num_parents_mating = 4

fitness_function = fitness_func

sol_per_pop = 8
num_genes = len(function_inputs)

init_range_low = -2
init_range_high = 5

parent_selection_type = "sss"
keep_parents = 1

crossover_type = "single_point"

mutation_type = "random"
mutation_percent_genes = 10

The `on_generation` Parameter¶

An optional parameter named on_generation is supported which allows the user to call a function (with a single parameter) after each generation. Here is a simple function that just prints the current generation number and the fitness value of the best solution in the current generation. The generations_completed attribute of the GA class returns the number of the last completed generation.

def on_gen(ga_instance):
    print("Generation : ", ga_instance.generations_completed)
    print("Fitness of the best solution :", ga_instance.best_solution()[1])

After being defined, the function is assigned to the on_generation parameter of the GA class constructor. By doing that, the on_gen() function will be called after each generation.

ga_instance = pygad.GA(...,
                       on_generation=on_gen,
                       ...)

After the parameters are prepared, we can import PyGAD and build an instance of the pygad.GA class.

Import `pygad`¶

The next step is to import PyGAD as follows:

import pygad

The pygad.GA class holds the implementation of all methods for running the genetic algorithm.

Create an Instance of the `pygad.GA` Class¶

The pygad.GA class is instantiated where the previously prepared parameters are fed to its constructor. The constructor is responsible for creating the initial population.

ga_instance = pygad.GA(num_generations=num_generations,
                       num_parents_mating=num_parents_mating,
                       fitness_func=fitness_function,
                       sol_per_pop=sol_per_pop,
                       num_genes=num_genes,
                       init_range_low=init_range_low,
                       init_range_high=init_range_high,
                       parent_selection_type=parent_selection_type,
                       keep_parents=keep_parents,
                       crossover_type=crossover_type,
                       mutation_type=mutation_type,
                       mutation_percent_genes=mutation_percent_genes)

Run the Genetic Algorithm¶

After an instance of the pygad.GA class is created, the next step is to call the run() method as follows:

ga_instance.run()

Inside this method, the genetic algorithm evolves over some generations by doing the following tasks:

Calculating the fitness values of the solutions within the current population.
Select the best solutions as parents in the mating pool.
Apply the crossover & mutation operation
Repeat the process for the specified number of generations.

Plotting Results¶

There is a method named plot_fitness() which creates a figure summarizing how the fitness values of the solutions change with the generations.

ga_instance.plot_fitness()

Information about the Best Solution¶

The following information about the best solution in the last population is returned using the best_solution() method.

Solution
Fitness value of the solution
Index of the solution within the population

solution, solution_fitness, solution_idx = ga_instance.best_solution()
print(f"Parameters of the best solution : {solution}")
print(f"Fitness value of the best solution = {solution_fitness}")
print(f"Index of the best solution : {solution_idx}")

Using the best_solution_generation attribute of the instance from the pygad.GA class, the generation number at which the best fitness is reached could be fetched.

if ga_instance.best_solution_generation != -1:
    print(f"Best fitness value reached after {ga_instance.best_solution_generation} generations.")

Saving & Loading the Results¶

After the run() method completes, it is possible to save the current instance of the genetic algorithm to avoid losing the progress made. The save() method is available for that purpose. Just pass the file name to it without an extension. According to the next code, a file named genetic.pkl will be created and saved in the current directory.

filename = 'genetic'
ga_instance.save(filename=filename)

You can also load the saved model using the load() function and continue using it. For example, you might run the genetic algorithm for some generations, save its current state using the save() method, load the model using the load() function, and then call the run() method again.

loaded_ga_instance = pygad.load(filename=filename)

After the instance is loaded, you can use it to run any method or access any property.

print(loaded_ga_instance.best_solution())

Life Cycle of PyGAD¶

The next figure lists the different stages in the lifecycle of an instance of the pygad.GA class. Note that PyGAD stops when either all generations are completed or when the function passed to the on_generation parameter returns the string stop.

The next code implements all the callback functions to trace the execution of the genetic algorithm. Each callback function prints its name.

import pygad
import numpy

function_inputs = [4,-2,3.5,5,-11,-4.7]
desired_output = 44

def fitness_func(ga_instance, solution, solution_idx):
    output = numpy.sum(solution*function_inputs)
    fitness = 1.0 / (numpy.abs(output - desired_output) + 0.000001)
    return fitness

fitness_function = fitness_func

def on_start(ga_instance):
    print("on_start()")

def on_fitness(ga_instance, population_fitness):
    print("on_fitness()")

def on_parents(ga_instance, selected_parents):
    print("on_parents()")

def on_crossover(ga_instance, offspring_crossover):
    print("on_crossover()")

def on_mutation(ga_instance, offspring_mutation):
    print("on_mutation()")

def on_generation(ga_instance):
    print("on_generation()")

def on_stop(ga_instance, last_population_fitness):
    print("on_stop()")

ga_instance = pygad.GA(num_generations=3,
                       num_parents_mating=5,
                       fitness_func=fitness_function,
                       sol_per_pop=10,
                       num_genes=len(function_inputs),
                       on_start=on_start,
                       on_fitness=on_fitness,
                       on_parents=on_parents,
                       on_crossover=on_crossover,
                       on_mutation=on_mutation,
                       on_generation=on_generation,
                       on_stop=on_stop)

ga_instance.run()

Based on the used 3 generations as assigned to the num_generations argument, here is the output.

on_start()

on_fitness()
on_parents()
on_crossover()
on_mutation()
on_generation()

on_fitness()
on_parents()
on_crossover()
on_mutation()
on_generation()

on_fitness()
on_parents()
on_crossover()
on_mutation()
on_generation()

on_stop()

Examples¶

This section gives the complete code of some examples that use pygad. Each subsection builds a different example.

Linear Model Optimization - Single Objective¶

This example is discussed in the Steps to Use PyGAD section which optimizes a linear model. Its complete code is listed below.

import pygad
import numpy

"""
Given the following function:
    y = f(w1:w6) = w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + 6wx6
    where (x1,x2,x3,x4,x5,x6)=(4,-2,3.5,5,-11,-4.7) and y=44
What are the best values for the 6 weights (w1 to w6)? We are going to use the genetic algorithm to optimize this function.
"""

function_inputs = [4,-2,3.5,5,-11,-4.7] # Function inputs.
desired_output = 44 # Function output.

def fitness_func(ga_instance, solution, solution_idx):
    output = numpy.sum(solution*function_inputs)
    fitness = 1.0 / (numpy.abs(output - desired_output) + 0.000001)
    return fitness

num_generations = 100 # Number of generations.
num_parents_mating = 10 # Number of solutions to be selected as parents in the mating pool.

sol_per_pop = 20 # Number of solutions in the population.
num_genes = len(function_inputs)

last_fitness = 0
def on_generation(ga_instance):
    global last_fitness
    print(f"Generation = {ga_instance.generations_completed}")
    print(f"Fitness    = {ga_instance.best_solution(pop_fitness=ga_instance.last_generation_fitness)[1]}")
    print(f"Change     = {ga_instance.best_solution(pop_fitness=ga_instance.last_generation_fitness)[1] - last_fitness}")
    last_fitness = ga_instance.best_solution(pop_fitness=ga_instance.last_generation_fitness)[1]

ga_instance = pygad.GA(num_generations=num_generations,
                       num_parents_mating=num_parents_mating,
                       sol_per_pop=sol_per_pop,
                       num_genes=num_genes,
                       fitness_func=fitness_func,
                       on_generation=on_generation)

# Running the GA to optimize the parameters of the function.
ga_instance.run()

ga_instance.plot_fitness()

# Returning the details of the best solution.
solution, solution_fitness, solution_idx = ga_instance.best_solution(ga_instance.last_generation_fitness)
print(f"Parameters of the best solution : {solution}")
print(f"Fitness value of the best solution = {solution_fitness}")
print(f"Index of the best solution : {solution_idx}")

prediction = numpy.sum(numpy.array(function_inputs)*solution)
print(f"Predicted output based on the best solution : {prediction}")

if ga_instance.best_solution_generation != -1:
    print(f"Best fitness value reached after {ga_instance.best_solution_generation} generations.")

# Saving the GA instance.
filename = 'genetic' # The filename to which the instance is saved. The name is without extension.
ga_instance.save(filename=filename)

# Loading the saved GA instance.
loaded_ga_instance = pygad.load(filename=filename)
loaded_ga_instance.plot_fitness()

Linear Model Optimization - Multi-Objective¶

This is a multi-objective optimization example that optimizes these 2 functions:

y1 = f(w1:w6) = w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + 6wx6
y2 = f(w1:w6) = w1x7 + w2x8 + w3x9 + w4x10 + w5x11 + 6wx12

Where:

(x1,x2,x3,x4,x5,x6)=(4,-2,3.5,5,-11,-4.7) and y=50
(x7,x8,x9,x10,x11,x12)=(-2,0.7,-9,1.4,3,5) and y=30

The 2 functions use the same parameters (weights) w1 to w6.

The goal is to use PyGAD to find the optimal values for such weights that satisfy the 2 functions y1 and y2.

To use PyGAD to solve multi-objective problems, the only adjustment is to return a list, tuple, or numpy.ndarray from the fitness function. Each element represents the fitness of an objective in order. That is the first element is the fitness of the first objective, the second element is the fitness for the second objective, and so on.

import pygad
import numpy

"""
Given these 2 functions:
    y1 = f(w1:w6) = w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + 6wx6
    y2 = f(w1:w6) = w1x7 + w2x8 + w3x9 + w4x10 + w5x11 + 6wx12
    where (x1,x2,x3,x4,x5,x6)=(4,-2,3.5,5,-11,-4.7) and y=50
    and   (x7,x8,x9,x10,x11,x12)=(-2,0.7,-9,1.4,3,5) and y=30
What are the best values for the 6 weights (w1 to w6)? We are going to use the genetic algorithm to optimize these 2 functions.
This is a multi-objective optimization problem.

PyGAD considers the problem as multi-objective if the fitness function returns:
    1) List.
    2) Or tuple.
    3) Or numpy.ndarray.
"""

function_inputs1 = [4,-2,3.5,5,-11,-4.7] # Function 1 inputs.
function_inputs2 = [-2,0.7,-9,1.4,3,5] # Function 2 inputs.
desired_output1 = 50 # Function 1 output.
desired_output2 = 30 # Function 2 output.

def fitness_func(ga_instance, solution, solution_idx):
    output1 = numpy.sum(solution*function_inputs1)
    output2 = numpy.sum(solution*function_inputs2)
    fitness1 = 1.0 / (numpy.abs(output1 - desired_output1) + 0.000001)
    fitness2 = 1.0 / (numpy.abs(output2 - desired_output2) + 0.000001)
    return [fitness1, fitness2]

num_generations = 100
num_parents_mating = 10

sol_per_pop = 20
num_genes = len(function_inputs1)

ga_instance = pygad.GA(num_generations=num_generations,
                       num_parents_mating=num_parents_mating,
                       sol_per_pop=sol_per_pop,
                       num_genes=num_genes,
                       fitness_func=fitness_func,
                       parent_selection_type='nsga2')

ga_instance.run()

ga_instance.plot_fitness(label=['Obj 1', 'Obj 2'])

solution, solution_fitness, solution_idx = ga_instance.best_solution(ga_instance.last_generation_fitness)
print(f"Parameters of the best solution : {solution}")
print(f"Fitness value of the best solution = {solution_fitness}")

prediction = numpy.sum(numpy.array(function_inputs1)*solution)
print(f"Predicted output 1 based on the best solution : {prediction}")
prediction = numpy.sum(numpy.array(function_inputs2)*solution)
print(f"Predicted output 2 based on the best solution : {prediction}")

This is the result of the print statements. The predicted outputs are close to the desired outputs.

Parameters of the best solution : [ 0.79676439 -2.98823386 -4.12677662  5.70539445 -2.02797016 -1.07243922]
Fitness value of the best solution = [  1.68090829 349.8591915 ]
Predicted output 1 based on the best solution : 50.59491545442283
Predicted output 2 based on the best solution : 29.99714270722312

This is the figure created by the plot_fitness() method. The fitness of the first objective has the green color. The blue color is used for the second objective fitness.

Reproducing Images¶

This project reproduces a single image using PyGAD by evolving pixel values. This project works with both color and gray images. Check this project at GitHub: https://github.com/ahmedfgad/GARI.

For more information about this project, read this tutorial titled Reproducing Images using a Genetic Algorithm with Python available at these links:

Project Steps¶

The steps to follow in order to reproduce an image are as follows:

Read an image
Prepare the fitness function
Create an instance of the pygad.GA class with the appropriate parameters
Run PyGAD
Plot results
Calculate some statistics

The next sections discusses the code of each of these steps.

Read an Image¶

There is an image named fruit.jpg in the GARI project which is read according to the next code.

import imageio
import numpy

target_im = imageio.imread('fruit.jpg')
target_im = numpy.asarray(target_im/255, dtype=float)

Here is the read image.

Based on the chromosome representation used in the example, the pixel values can be either in the 0-255, 0-1, or any other ranges.

Note that the range of pixel values affect other parameters like the range from which the random values are selected during mutation and also the range of the values used in the initial population. So, be consistent.

Prepare the Fitness Function¶

The next code creates a function that will be used as a fitness function for calculating the fitness value for each solution in the population. This function must be a maximization function that accepts 3 parameters representing the instance of the pygad.GA class, a solution, and its index. It returns a value representing the fitness value.

import gari

target_chromosome = gari.img2chromosome(target_im)

def fitness_fun(ga_instance, solution, solution_idx):
    fitness = numpy.sum(numpy.abs(target_chromosome-solution))

    # Negating the fitness value to make it increasing rather than decreasing.
    fitness = numpy.sum(target_chromosome) - fitness
    return fitness

The fitness value is calculated using the sum of absolute difference between genes values in the original and reproduced chromosomes. The gari.img2chromosome() function is called before the fitness function to represent the image as a vector because the genetic algorithm can work with 1D chromosomes.

The implementation of the gari module is available at the GARI GitHub project and its code is listed below.

import numpy
import functools
import operator

def img2chromosome(img_arr):
    return numpy.reshape(a=img_arr, newshape=(functools.reduce(operator.mul, img_arr.shape)))

def chromosome2img(vector, shape):
    if len(vector) != functools.reduce(operator.mul, shape):
        raise ValueError(f"A vector of length {len(vector)} into an array of shape {shape}.")

    return numpy.reshape(a=vector, newshape=shape)

Create an Instance of the `pygad.GA` Class¶

It is very important to use random mutation and set the mutation_by_replacement to True. Based on the range of pixel values, the values assigned to the init_range_low, init_range_high, random_mutation_min_val, and random_mutation_max_val parameters should be changed.

If the image pixel values range from 0 to 255, then set init_range_low and random_mutation_min_val to 0 as they are but change init_range_high and random_mutation_max_val to 255.

Feel free to change the other parameters or add other parameters. Please check the PyGAD’s documentation for the full list of parameters.

import pygad

ga_instance = pygad.GA(num_generations=20000,
                       num_parents_mating=10,
                       fitness_func=fitness_fun,
                       sol_per_pop=20,
                       num_genes=target_im.size,
                       init_range_low=0.0,
                       init_range_high=1.0,
                       mutation_percent_genes=0.01,
                       mutation_type="random",
                       mutation_by_replacement=True,
                       random_mutation_min_val=0.0,
                       random_mutation_max_val=1.0)

Run PyGAD¶

Simply, call the run() method to run PyGAD.

ga_instance.run()

Plot Results¶

After the run() method completes, the fitness values of all generations can be viewed in a plot using the plot_fitness() method.

ga_instance.plot_fitness()

Here is the plot after 20,000 generations.

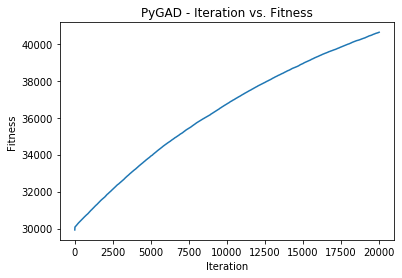
Calculate Some Statistics¶

Here is some information about the best solution.

# Returning the details of the best solution.
solution, solution_fitness, solution_idx = ga_instance.best_solution()
print(f"Fitness value of the best solution = {solution_fitness}")
print(f"Index of the best solution : {solution_idx}")

if ga_instance.best_solution_generation != -1:
    print(f"Best fitness value reached after {ga_instance.best_solution_generation} generations.")

result = gari.chromosome2img(solution, target_im.shape)
matplotlib.pyplot.imshow(result)
matplotlib.pyplot.title("PyGAD & GARI for Reproducing Images")
matplotlib.pyplot.show()

Evolution by Generation¶

The solution reached after the 20,000 generations is shown below.

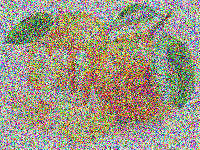
After more generations, the result can be enhanced like what shown below.

The results can also be enhanced by changing the parameters passed to the constructor of the pygad.GA class.

Here is how the image is evolved from generation 0 to generation 20,000s.

Generation 0

Generation 1,000

Generation 2,500

Generation 4,500

Generation 7,000

Generation 8,000

Generation 20,000

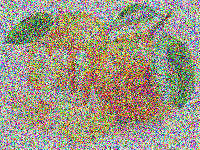
Clustering¶

For a 2-cluster problem, the code is available here. For a 3-cluster problem, the code is here. The 2 examples are using artificial samples.

Soon a tutorial will be published at Paperspace to explain how clustering works using the genetic algorithm with examples in PyGAD.

CoinTex Game Playing using PyGAD¶

The code is available the CoinTex GitHub project. CoinTex is an Android game written in Python using the Kivy framework. Find CoinTex at Google Play: https://play.google.com/store/apps/details?id=coin.tex.cointexreactfast

Check this Paperspace tutorial for how the genetic algorithm plays CoinTex: https://blog.paperspace.com/building-agent-for-cointex-using-genetic-algorithm. Check also this YouTube video showing the genetic algorithm while playing CoinTex.

pygad Module¶

pygad.GA Class¶

__init__()¶

Plotting Methods in pygad.GA Class¶

Class Attributes¶

Other Instance Attributes & Methods¶

Other Attributes¶

Other Methods¶

initialize_population()¶

cal_pop_fitness()¶

run()¶

Parent Selection Methods¶

steady_state_selection()¶

rank_selection()¶

random_selection()¶

tournament_selection()¶

roulette_wheel_selection()¶

stochastic_universal_selection()¶

nsga2_selection()¶

tournament_selection_nsga2()¶

Crossover Methods¶

single_point_crossover()¶

two_points_crossover()¶

uniform_crossover()¶

scattered_crossover()¶

Mutation Methods¶

random_mutation()¶

swap_mutation()¶

inversion_mutation()¶

scramble_mutation()¶

adaptive_mutation()¶

best_solution()¶

plot_fitness()¶

plot_new_solution_rate()¶

plot_genes()¶

save()¶

Functions in pygad¶

pygad.load()¶

Steps to Use pygad¶

Preparing the fitness_func Parameter¶

Preparing Other Parameters¶

The on_generation Parameter¶

Import pygad¶

Create an Instance of the pygad.GA Class¶

Run the Genetic Algorithm¶

Plotting Results¶

Information about the Best Solution¶

Saving & Loading the Results¶

Life Cycle of PyGAD¶

Examples¶

Linear Model Optimization - Single Objective¶

Linear Model Optimization - Multi-Objective¶

Reproducing Images¶

Project Steps¶

Read an Image¶

Prepare the Fitness Function¶

Create an Instance of the pygad.GA Class¶

Run PyGAD¶

Plot Results¶

Calculate Some Statistics¶

Evolution by Generation¶

Clustering¶

CoinTex Game Playing using PyGAD¶

`pygad` Module¶

`pygad.GA` Class¶

`init()`¶

Plotting Methods in `pygad.GA` Class¶

`initialize_population()`¶

`cal_pop_fitness()`¶

`run()`¶

`steady_state_selection()`¶

`rank_selection()`¶

`random_selection()`¶

`tournament_selection()`¶

`roulette_wheel_selection()`¶

`stochastic_universal_selection()`¶

`nsga2_selection()`¶

`tournament_selection_nsga2()`¶

`single_point_crossover()`¶

`two_points_crossover()`¶

`uniform_crossover()`¶

`scattered_crossover()`¶

`random_mutation()`¶

`swap_mutation()`¶

`inversion_mutation()`¶

`scramble_mutation()`¶

`adaptive_mutation()`¶

`best_solution()`¶

`plot_fitness()`¶

`plot_new_solution_rate()`¶

`plot_genes()`¶

`save()`¶

Functions in `pygad`¶

`pygad.load()`¶

Steps to Use `pygad`¶

Preparing the `fitness_func` Parameter¶

The `on_generation` Parameter¶

Import `pygad`¶

Create an Instance of the `pygad.GA` Class¶

Create an Instance of the `pygad.GA` Class¶